Drawing shapes in Pycairo

In a previous article we learnt how to draw a rectangle in Pycairo. Here we cover other simple shapes.

Paths

The way Pycairo draws is to first define a path and then draw it by either filling or outlining the path (or both). In the previous article we just used the rectangle function to create a single rectangle. But in fact paths can be more complex that that. A path can consist of connected lines and curves that create a more complex shape. A path can also contain more than one shape. You can even place one path inside another to create a hole.

Lines

You can draw a line by specifying the two end points. You use move_to to specify the star of the path (the first point) and then line_to to draw a line to the second point:

ctx.move_to(1, 1)
ctx.line_to(2.5, 1.5)

ctx.set_source_rgb(1, 0, 0)
ctx.set_line_width(0.06)
ctx.stroke()

This code draws a line from point (1, 1) to point (2.5, 1.5) in our user coordinates (see the previous article). The full code is here:

import cairo

WIDTH = 3
HEIGHT = 2
PIXEL_SCALE = 100

surface = cairo.ImageSurface(cairo.FORMAT_RGB24,
                             WIDTH*PIXEL_SCALE,
                             HEIGHT*PIXEL_SCALE)
ctx = cairo.Context(surface)
ctx.scale(PIXEL_SCALE, PIXEL_SCALE)

ctx.rectangle(0, 0, WIDTH, HEIGHT)
ctx.set_source_rgb(0.8, 0.8, 1)
ctx.fill()

# Drawing code
ctx.move_to(1, 1)
ctx.line_to(2.5, 1.5)

ctx.set_source_rgb(1, 0, 0)
ctx.set_line_width(0.06)
ctx.stroke()
# End of drawing code

surface.write_to_png('line.png')

For the rest of this article we will only show the drawing code, the surrounding code is the same for every example.

Polygons

The simplest shapes to draw are polygons - a set of straight lines. They are drawn in a similar way to lines - move to the first point, line to the second point, line to the third point as so on. You only need a move to for the first point, the path automatically continues each new line from the end of the previous line. After the final point you should call close_path - this automatically adds the final line from the last point back to the first point, closing the shape.

Here is the code to draw a polygon, actually a pentagon:

ctx.move_to(1, 0.5)
ctx.line_to(2, 0.5)
ctx.line_to(2.2, 1.3)
ctx.line_to(1.5, 1.7)
ctx.line_to(0.8, 1.3)
ctx.close_path()

ctx.set_source_rgb(1, 0.5, 0)
ctx.fill_preserve()

ctx.set_source_rgb(1, 1, 0)
ctx.set_line_width(0.04)
ctx.stroke()

Arcs and pie charts

You can draw an arc (part of the circumference of a circle) using the arc function. This takes the following parameters:

• cx - the x coordinate of the centre of the circle
• cy - the y coordinate of the centre of the circle
• radius - the radius of the circle
• start_angle - the start angle of the arc
• end_angle - the end angle of the arc

The start and end angles are measured in radians (2*pi radians = 360 degrees, a full circle). The positive x axis is angle 0, and angles are measured in the clockwise direction. So for example start angle 0 and end angle pi/2 defines the bottom right quarter of a circle.

Here is the code to draw an arc, a segment and a sector (pie wedge):

#arc
ctx.arc(0.5, 0.2, 0.5, 0, math.pi/2)
ctx.set_source_rgb(0, 0, 0)
ctx.set_line_width(0.04)
ctx.stroke()

#segment
ctx.arc(1, 1.2, 0.5, 0, math.pi/2)
ctx.close_path()
ctx.set_source_rgb(1, 0, 0)
ctx.fill()

#sector
ctx.move_to(2, 0.2)
ctx.arc(2, 0.2, 0.5, 0, math.pi/2)
ctx.close_path()
ctx.set_source_rgb(0, 1, 0)
ctx.fill()

The black curve is a simple arc. It is just a curved line, not a shape, so we just stroke it.

The red shape is a segment. To create a segment, we just draw the arc as before. Then we close the path. Pycairo adds a line from the end point (the end of the arc) back to the start point (the start of the arc).

The green shape is a sector, useful as a wedge in a pie chart. To draw this we first move_to the centre of the circle. Then when we call arc, Pycairo automatically adds a line from the centre of the circle to the start of the arc. Finally when we call close_path it adds another line back to the start of the path - in this case, the centre of the circle. This creates a pie wedge.

arc measures angles in a clockwise direction. In maths, we usually measure angles in an anticlockwise direction. If you prefer to do that, you can use the arc_negative function, that is identical to arc except that it measures angles anticlockwise.

Circles

In Pycairo, you draw a circle by creating an arc with a start angle of 0 and and end angle of 2*pi radians (ie 360 degrees).

To draw a circle with centre (2, 1) and radius 0.5 you create the following arc:

ctx.arc(2, 1, 0.5, 0, 2*math.pi)

Bezier curves

A Bezier curve is a very versatile curve with some useful mathematical properties. Most vector drawing programs support Bezier curves. This section doesn't cover them in great detail, if you are not familiar with them it is a good idea to use a program such as Inkscape to play around and see how they work.

A Bezier curve is controlled by 4 points:

• the start point (sx, sy)
• two control points (c1x, c1y) and (c2x, c2y)
• the end point (ex, ey)

It is created using the curve_to function:

curve_to(c1x, c1y, c2x, c2y, ex, ey)

Notice that the function does not specify the start point. It will automatically start at the current point (the point where the previous line or curve ended). This is the same as the line_to function.

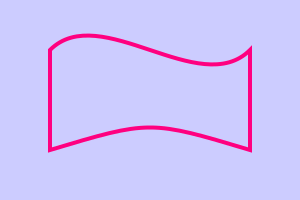
Here is a shape drawn with 2 Bezier curves and 2 straight lines:

ctx.move_to(0.5, 0.5)
ctx.curve_to(1, 0, 2, 1, 2.5, 0.5)
ctx.line_to(2.5, 1.5)
ctx.curve_to(1.5, 1.2, 1.5, 1.2, 0.5, 1.5)
ctx.close_path()
ctx.set_source_rgb(1, 0, 0.5)
ctx.set_line_width(0.04)
ctx.stroke()

More complex paths

A path does not have to consist of a single shape. One path can contain multiple disconnected shapes. Here is an example:

ctx.move_to(0.9, 0.5)
ctx.line_to(1.4, 1)
ctx.line_to(0.9, 1.5)
ctx.line_to(0.4, 1)
ctx.close_path()

ctx.move_to(2.1, 0.5)
ctx.line_to(2.6, 1)
ctx.line_to(2.1, 1.5)
ctx.line_to(1.6, 1)
ctx.close_path()

ctx.set_source_rgb(0.5, 1, 0)
ctx.fill()

What is happening here? Well the first block of code creates a diamond shape, in the normal way.

The next block of code draws another diamond, in a different position. We didn't fill or stroke the first path, so it is still there, and the second path gets added to it. This creates one path that contains two separate shapes. Each shape is called a subpath.

In this case, the second call to move_to automatically creates a new subpath - this is the usual way of creating subpaths. If for some reason you needed to create a new subpath without calling the move_to function, you could use the new_sub_path function instead.

Now when we call fill the entire path (ie both subpaths) is filled.

Subpaths are useful if you want to fill several shapes with a gradient or pattern. Using subpaths means the gradient or pattern will be aligned between the different shapes.

You can also use subpaths to create shapes with holes in them. To do this, simply create a subpath with another subpath completely inside it:

ctx.move_to(0.5, 0.4)
ctx.line_to(2.5, 0.4)
ctx.line_to(2.5, 1.6)
ctx.line_to(0.5, 1.6)
ctx.close_path()

ctx.move_to(1.5, 0.5)
ctx.line_to(2, 1)
ctx.line_to(1.5, 1.5)
ctx.line_to(1, 1)
ctx.close_path()

ctx.set_source_rgb(0, 0.5, 0)
ctx.set_fill_rule(cairo.FILL_RULE_EVEN_ODD)
ctx.fill()

In this code, we first draw a rectangle. Then we create a second subpath with a diamond shape that is entirely inside the rectangle.

We also set the fill rule to even odd. This means that any area that is inside an odd number of subpaths will be filled, any area that is inside an even number of subpaths will be unfilled.

In this case, the area that is inside the rectangle but not inside the diamond is filled (it is inside 1 path, an odd numer). The area that is inside the rectangle and inside the diamond is not filled (it is inside 2 paths, and even number).

See also

• Paths and complex shapes in Pycairo
• Bezier curves in Pycairo