Operator overloading
Categories: magic methods

Operator overloading allows us to add functionality to our own classes so that they can support standard Python operators such as +, -, etc.
We will illustrate this using the example class Matrix, a 2 by 2 matrix.
Adding two matrices
In high school maths, we learned how to add two matrices. If we wanted to do this in Python, the most obvious way to do this would be to define an add function:
p = Matrix(1, 2, 3, 4)
q = Matrix(5, 6, 7, 8)
r = p.add(q)
That is ok, but it would be nice if we could write:
p = Matrix(1, 2, 3, 4)
q = Matrix(5, 6, 7, 8)
r = p + q
Well we can! In fact, we can override all the arithmetic operators if we wish. In this section, we will look at +, -, and *, but the technique can apply to any operator.
How matrix addition works
Just to recap the basics of matrix algebra, the sum of two matrices:
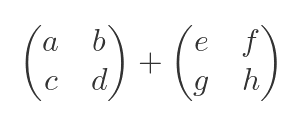
is:
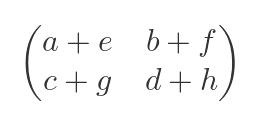
So in our example, the expected result would be:
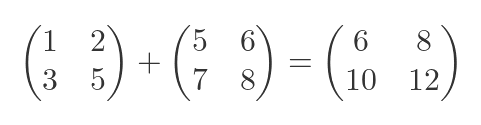
Overloading the addition operator
We can override the addition operator for a class by providing an __add__ method:
class Matrix:
def __init__(self, a, b, c, d):
self.data = [a, b, c, d]
def __add__(self, other):
if isinstance(other, Matrix):
return Matrix(self.data[0] + other.data[0],
self.data[1] + other.data[1],
self.data[2] + other.data[2],
self.data[3] + other.data[3])
else:
return NotImplemented
The __add__ method accepts a parameter other. We first check if other is a Matrix. If it is, the method creates a brand new Matrix object whose elements are formed by adding the elements of other to self.
If other is not a Matrix, our code doesn't know how to handle it. In that case, we must return NotImplemented. Python can then decide what to do (this is covered in more detail below).
Here is how this is used:
p = Matrix(1, 2, 3, 4)
q = Matrix(5, 6, 7, 8)
r = p + q
print(r)
We create two matrices, p and q. We then perform the calculation p + q. This calls the __add__ method on the first object p, passing the second object r as the other parameter.
The __add__ function returns a Matrix that is the result of the addition, and this gets assigned to r. The result is printed:
[6, 8][10, 12]
Negation
We could also implement matrix subtraction by overriding the - operator. We do this by adding a __sub__ method that works in a similar way to __add__, but subtracts instead. We won't show that here, it is very similar to the addition code above.
But the - operator has a second meaning, it can be used to negate a value. For example if a = 5 then -a = -5. We say negation is a unary operator, because it works on a single value. For a matrix, it works like this:
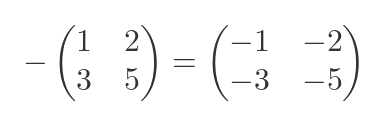
We can add support for negation by defining an __neg__ method like this:
class Matrix:
def __init__(self, a, b, c, d):
self.data = [a, b, c, d]
def __neg__(self):
return Matrix(-self.data[0],
-self.data[1],
-self.data[2],
-self.data[3])
We simply return a new matrix that negates the values of the existing matrix. Notice that the __neg__ method doesn't accept an other parameter (because it is a unary operator), and it cannot fail with a NotImplemented error because every matrix can be negated.
Of course, for a fully implemented Matrix class, we should support subtraction and negation. To do this, we just need to implement __sub__ and __neg__. When the Python interpreter encounters a - sign applied to a Matrix, it will decide whether it is subtraction or negation, and call the correct method. Our code doesn't need to worry about that, it is the Python interpreter's job.
Matrix multiplication
Matrix multiplication is a more interesting case, because you can multiply a matrix by another matrix, or alternatively you can multiply it by a scalar (ie an ordinary number).
Multiplying a matrix by a matrix
The product of two matrices:
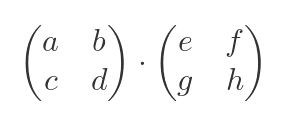
is:
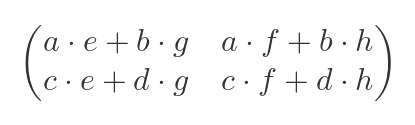
Multiplying a matrix by a scalar
You can also multiply a matrix by a scalar (an ordinary number n):
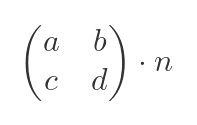
giving:
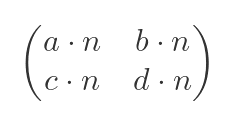
Overloading the multiply operator
Here is a version of the Matrix class with an implementation of __mul__ (which gets called for any multiply operation involving a matrix):
class Matrix:
def __init__(self, a, b, c, d):
self.a = a
self.b = b
self.c = c
self.d = d
def __mul__(self, other):
if isinstance(other, (int, float)):
return Matrix(self.data[0] * other,
self.data[1] * other,
self.data[2] * other,
self.data[3] * other)
elif isinstance(other, Matrix):
return Matrix(self.data[0] * other.data[0] + self.data[1] * other.data[1],
self.data[0] * other.data[1] + self.data[1] * other.data[3],
self.data[2] * other.data[0] + self.data[3] * other.data[1],
self.data[2] * other.data[1] + self.data[3] * other.data[3])
else:
return NotImplemented
If you look at __mul__, you will see that the first thing we do is to check if other is a scalar. We do this by checking if it is an instance of int or float (you could also check other number types, such as complex, if you want the Matrix class to support them, but we won't do that in this example).
If the value is a number, we execute the code for the scalar multiplication equation above.
If the value is not a scalar, we check if it is a Matrix, and execute the code for the matrix multiplication equation above.
If the value is neither a number nor a Matrix, we return NotImplemented.
Here is an example:
p = Matrix(1, 2, 3, 4)
q = Matrix(5, 6, 7, 8)
print(p*2)
print(p*q)
This prints
[2, 4][6, 8]
[17, 22][39, 50]
As expected.
Reversing the arguments
What if we try to do this:
print(2*p)
Unfortunately, our existing code doesn't quite cope with this situation. We get an error:
TypeError: unsupported operand type(s) for *: 'int' and 'Matrix'
So what has happened here? We are trying to multiply 2*p:
- Python looks at the first value, 2, which is an
int. - It calls
int.__mul__passing in the second valuep, which is aMatrix. - Since
intis a built-in type, its__mul__function knows nothing about ourMatrixtype, so it returnsNotImplemented.
You might think that Python would give an error at this point, but actually, it tries one last thing:
- Python checks if the second argument
phas a__rmul__method. If not, it gives an error. - It calls
p.__rmul__passing in the first value 2. - If
p.__rmul__can handle an integer type, the value will be calculated. - If not,
p.__rmul__returnsNotImplementedand Python gives an error.
So, we can handle this extra case by implementing __rmul__ for our Matrix class:
def __rmul__(self, other):
if isinstance(other, (int, float)):
return Matrix(self.data[0] * other,
self.data[1] * other,
self.data[2] * other,
self.data[3] * other)
else:
return NotImplemented
In this case, self is the second operand p, and other is the first operand 2. This is because __rmul__ reverses the arguments.
Since other is an int, our code executes and creates the correct result. In this case, the code for handling numbers is identical in __mul__ and __rmul__ because for matrices, p*2 and 2*p are the same. That won't be true for all data types and all operators, of course.
Notice that if both operands are of type Matrix, the case will always be handled by __mul__, so there is no need to handle that case in __rmul__. This is generally true for all data types and operators.
Error checking
What if we try something crazy like, multiplying a matrix p by a string value:
print(p*'abc')
Our __mul__ code checks the type of the other value. It isn't a number, it isn't a Matrix, so we return NotImplemented.
Python will then check if str has an __rmul__ method. It does, but it can't handle our Matrix type, so again it returns NotImplemented. Python gives an error in that situation, as you would expect, because the expression cannot be evaluated.
In-place operators
There is an additional case to consider, the in-place operators such as += and *=. They are covered in a separate article
Summary of operators
Here is a summary of the available numerical operators:
| Method | Symbol |
|---|---|
| __add__ | + |
| __sub__ | - |
| __mul__ | * |
| __matmul__ | @ |
| __truediv__ | / |
| __floordiv__ | // |
| __mod__ | % |
| __divmod__ | |
| __pow__ | ** |
| __lshift__ | << |
| __rshift__ | >> |
| __and__ | & |
| __xor__ | ^ |
| __or__ | | |
| __neg__ | - |
| __pos__ | + |
Some of these need a bit more explanation:
__truediv__corresponds to the/operator, which usually results in a floating point value.__floordiv__corresponds to the//operator which usually results in an integer value. If you want your class to support both types of division, you must implement both methods. For ourMatrixclass, we might decide that only true division is required.__matmul__, the@operator, is a special operator that is not implemented by any of the Python built-in types. It is called__matmul__because it is used by NumPy to implement matrix multiplication. But it can be used for anything, so if you have a class that has a special operation that doesn't match any of the other magic methods, you can use__matmul__.__divmod__is a magic method that doesn't correspond to any existing Python symbol. The built-in functiondivmod(a, b)returns two values, the floor dividea//band the modulusa%b. If you implement this method, your class will work correctly when it is passed into thedivmodfunction.__neg__is a unary-operator, as discussed earlier.__pos__is a unary+operator. It is included as the equivalent of__neg__for the+operator. In most cases, it has no effect, for example, +3 is exactly the same as 3. If you write your own classes, it is possible to give+a special meaning, so that+xwill affect the value ofx, although this could cause confusion because the operator usually has no effect.
Related articles
Join the GraphicMaths/PythonInformer Newsletter
Sign up using this form to receive an email when new content is added to the graphpicmaths or pythoninformer websites:

Popular tags
2d arrays abstract data type and angle animation arc array arrays bar chart bar style behavioural pattern bezier curve built-in function callable object chain circle classes close closure cmyk colour combinations comparison operator context context manager conversion count creational pattern data science data types decorator design pattern device space dictionary drawing duck typing efficiency ellipse else encryption enumerate fill filter for loop formula function function composition function plot functools game development generativepy tutorial generator geometry gif global variable greyscale higher order function hsl html image image processing imagesurface immutable object in operator index inner function input installing integer iter iterable iterator itertools join l system lambda function latex len lerp line line plot line style linear gradient linspace list list comprehension logical operator lru_cache magic method mandelbrot mandelbrot set map marker style matplotlib monad mutability named parameter numeric python numpy object open operator optimisation optional parameter or pandas path pattern permutations pie chart pil pillow polygon pong positional parameter print product programming paradigms programming techniques pure function python standard library range recipes rectangle recursion regular polygon repeat rgb rotation roundrect scaling scatter plot scipy sector segment sequence setup shape singleton slicing sound spirograph sprite square str stream string stroke structural pattern symmetric encryption template tex text tinkerbell fractal transform translation transparency triangle truthy value tuple turtle unpacking user space vectorisation webserver website while loop zip zip_longest
